NeuralMorse — Reinventing Morse Code with Neural Networks
I redesigned Morse code with modern statistical techniques, including neural networks. NeuralMorse dynamically tokenizes input text and encodes it as sequences of eight tonal alphabets, optimized by word embeddings and the assignment problem.
tl;dr
I redesigned Morse code with modern statistical techniques, including neural networks—and this is what it sounds like:
Introduction
I love Morse code. The idea of encoding natural language using just two elements has fascinated me since I was a teenager. Even though it may have fallen out of fashion and is no longer widely used, the invention strikes as a beautiful combination of information theory and linguistics, and it even has some musical taste to it.

In Morse code, every letter is transmitted as a sequence of just two elements—dots and dashes. It is designed so that natural language text is transmitted as efficiently as possible. The length of each symbol (a sequence of elements) is roughly inversely proportional to the frequency of corresponding letter. For example, the most frequent letter in English, “e” is encoded as just a single dot, while it takes four elements (dash dash dot dash) to encode the less frequent letter “q.”
Still, I couldn’t help but wonder: could it be even more efficient?
For example, in English, the word “the” appears far more often than the letter “q” does. Communication would be more efficient if we dynamically tokenized the text and assigned shorter symbols to frequent tokens like “the,” and longer ones to rare characters like “q.” Also, if we allowed more than two elements (for example, with different lengths and pitches) instead of just dots and dashes, we could compress even more information into a fixed unit of time.
What if we reimagined Morse code using modern statistical techniques? That question led me to design NeuralMorse—a scheme that encodes text in a way similar to Morse code, but built using neural networks to maximize efficiency.
Desiderata
It’s tempting to dive right in and start assigning symbols—like giving “the” its own special code, for example—but that kind of ad-hoc design is unlikely to lead anywhere meaningful. Let’s first write out some desirable properties we want NeuralMorse to have, and go from there. We want NeuralMorse to:
- Encode text as sequences of a small number of “alphabets” (just like Morse code, but more elements).
- Represent both words and individual characters as symbols.
- Encode English text as efficiently as possible.
- Assign similar codes to semantically similar words.
- Sound musically pleasant (if possible).
Elements
How many elements should NeuralMorse use to encode text? Using just two wouldn’t be much different from Morse code, while seven might be too many. Solresol—a constructed language that uses the seven notes of the C major scale to express meaning and one of the inspirations for NeuralMorse—has faced criticism for being too difficult to use, especially for people without musical training or absolute pitch.
I settled on a total of eight elements: four different pitches, each with two durations:
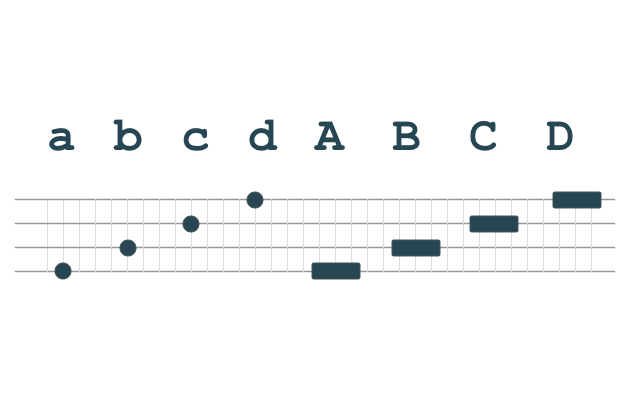
The capitalized elements (A, B, C, D) have the same pitches as their lower-case counterparts (a, b, c, d) but are three times longer in duration, just like the dots and dashes in Morse code. I believe most people can distinguish four distinct pitches, especially if they’re spaced appropriately, even without musical training.
Note that these different elements can be realized as any separate pitches you like, or even via different modalities of communication altogether. For example, they can be encoded as different pitches of sound, or different colors of light, or even different types of smoke. NeuralMorse doesn’t specify how exactly elements should be produced, as long as they are something that the communicators can encode and decode consistently.
In the rest of this article and in my implementation, I use four specific pitches:
| Element | Pitch |
|---|---|
| a / A | E4 |
| b / B | A4 (= 440 Hz) |
| c / C | B4 |
| d / D | E5 |
This sounds like the A pentatonic scale and I found it musically pleasant (see note 1), but I'm open to suggestions if you find any interesting encoding schemes for these elements.
Symbols
By combining these eight elements, we can form symbols, like the ones shown below:
| Symbol | Length |
|---|---|
| a | 1 |
| B | 3 |
| aB | 5 |
| dcba | 7 |
| BaC | 9 |
| ... | ... |
As with Morse code, the interval between elements is equal to the duration of a dot—the same length as elements a, b, c, and d. So the total duration of a symbol is the sum of its elements’ lengths, plus the time between them (equal to the number of elements minus one).
If we enumerate all possible symbols made from these eight elements with a total length of 9 or fewer, we get 1,800 unique combinations. Let’s call this set of 1,800 basic symbols. A sample of them is shown below:
| Symbol | Length |
|---|---|
| a | 1 |
| ... | ... |
| D | 3 |
| aa | 3 |
| ab | 3 |
| ... | ... |
| Aa | 5 |
| ... | ... |
| Dd | 5 |
| aaa | 5 |
| ... | ... |
| aaaa | 7 |
| aaab | 7 |
| ... | ... |
1,800 may sound like a lot, but I think it’s a manageable number with enough training. If you treat them as “basic words,” the size is comparable to foundational vocabulary sets in many languages. For example, basic English vocabulary lists often contain 1,000–2,000 words. In countries where Chinese characters are used (such as China and Japan), elementary school students typically learn 1,000–2,000 characters by the end of sixth grade.
Encoding Words and Characters Efficiently
Now, we need to think about how we can encode words and characters efficiently in NeuralMorse. This was probably the easiest part—this is a classic NLP problem where the goal is to represent text with a shortest sequence of words and characters defined by a dictionary of a fixed size.
For NeuralMorse, I used SentencePiece, a software toolkit commonly used for tokenizing natural language text in neural network preprocessing. It trains a statistical model that tokenizes and detokenizes input text in such a way that it minimizes the total length of codes required to encode the text, given a predetermined vocabulary size. For example, common words such as “the” and “you” are assigned their own tokens, whereas rarer words such as “neuroscience” and “serendipity” are broken down into smaller parts called subword units.
SentencePiece achieves this by training a unigram language model on a large corpus of plain text—typically drawn from web crawls, Wikipedia dumps, and other public datasets. After normalizing the input by lowercasing it, I trained a SentencePiece model using a vocabulary of 1,900 tokens (see note 2) on the OpenWebText2 corpus—specifically, a 1/100th sample (see note 3).
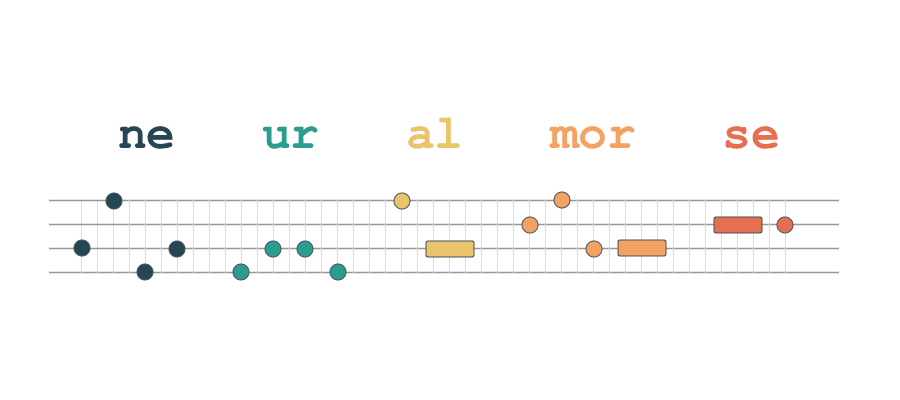
Here’s an example of how the model tokenizes the sentence "NeuralMorse is a method for encoding natural language text as sequences of eight tonal alphabets" (“▁” indicates whitespace):
ne ur al mor se ▁ is ▁ a ▁ method ▁ for ▁ en co ding ▁ natural ▁ language ▁ text
▁ as ▁ s equ ence s ▁ of ▁ eight ▁ to n al ▁ al ph ab et s
You’ll notice that words like “is,” “method,” and “language” are assigned as individual tokens, while words like “neural” and “sequence” are broken down into subwords like “ne/ur/al” and “s/equ/ence.” The vocabulary includes all single letters (a–z), digits (0–9), and various punctuation marks (. , ! ? etc.), so the model can always fall back on character-level encoding for unknown or rare words.
Making Words with Similar Meanings Sound Similar
At this point, we could simply assign each of the 1,800 basic symbols to the tokens learned via SentencePiece, based on frequency: more frequent tokens get shorter symbols. However, this approach produces an essentially random mapping, like the one below:
| Token | Symbol |
|---|---|
| natural | bDac |
| october | Abcd |
| government | Cdac |
| american | dDcd |
| etc. |
This randomness may be acceptable—after all, the original Morse code assignments don’t seem particularly systematic either. But trying to memorize 1,800 token–symbol pairs with no meaningful structure would be challenging. Moreover, many symbols have the same length. For example, there are 1,216 different symbols that are 9 dots long, such as Aaaa, aAaa, and AAa. We need a more meaningful way to break these ties.
Natural languages often have some correlation between a word’s meaning and how it sounds. For instance, adjectives in Japanese typically end with “-i,” and in Esperanto with “-a.” In English, we have morphological patterns like “recent” vs. “recently” and “success” vs. “successful.” These patterns make it easier to learn and remember words, even though they are technically distinct words. Therefore, in terms of the learning cost and experience of NeuralMorse, it’d probably be better if related words sound somewhat similar (i.e. they are assigned similar symbols).
So how do we make that happen? This is where the neural network comes in.
I trained word embeddings—real-valued vector representations that capture semantic meaning—for all the tokens from the SentencePiece model. Using fastText, I trained a Skip-gram model on a larger corpus (a 1/10th sample of OpenWebText2, which contains about 2.5 billion words). Then I applied agglomerative clustering to build a dendrogram and converted it into binary sequences representing how tokens branch from the root.
By sorting tokens by these binary codes, we get this beautiful list of tokens sorted and arranged by their meanings:
| Token | Code |
|---|---|
| nothing | 000100000 |
| something | 0001000010 |
| anything | 0001000011 |
| someone | 0001000100 |
| anyone | 0001000101 |
| everything | 0001000110 |
| everyone | 0001000111 |
| ... | ... |
| february | 10110111011 |
| april | 1011011110 |
| june | 1011011111 |
| 2020 | 1011100 |
| 2021 | 1011101 |
| 2019 | 10111100 |
| ... | ... |
| york | 11101001100 |
| washington | 11101001101 |
| ville | 11101001110 |
| california | 111010011110 |
| texas | 1110100111110 |
| florida | 1110100111111 |
| ... | ... |
You can also represent symbols in binary form by encoding each element: a = 000, b = 001, ..., D = 111, and concatenating them.
| Symbol | Code |
|---|---|
| ac | 000010 |
| cc | 010010 |
| C | 110 |
| cab | 010000001 |
| bcc | 001010010 |
| Cb | 110001 |
| ... | ... |
| Db | 111001 |
| add | 000011011 |
| dbd | 011001011 |
| cdba | 010011001000 |
| cbbc | 010001001010 |
| ddcd | 011011010011 |
| ... | ... |
Now you can measure the distance between any symbols and tokens by comparing corresponding codes and counting the number of different digits starting from the first one.
Putting It All Together
Finally, how can we assign symbols to tokens so that (1) frequent tokens are assigned shorter symbols and (2) tokens with similar meanings are assigned similar-sounding symbols? These two goals often conflict: prioritizing frequency may result in arbitrary symbol assignments for semantically related tokens, while prioritizing semantic similarity may compromise compression efficiency. The goal is to strike a reasonable balance.
Specifically, for token $t$ and its corresponding symbol $s$, we’d like to minimize the following cost function:
$$ \sum_{(t, s)} c(t, s) = \sum_{(t, s)} dist(code(t), code(s)) + \alpha * freq(t) * len(s) $$
- $code(t), code(s)$ are the binary code generated for token $t$ and symbol $s$
- $dist()$ is the Hamming distance between the codes
- $freq(t)$ is the normalized frequency of token $t$
- $len(s)$ is the length of symbol $s$, measured in dot-units
- $\alpha$ is a balancing coefficient to keep both terms on comparable scales
The first term corresponds to condition (2) while the second corresponds to (1). Now, all we need to do is find the assignment between symbols and tokens that minimizes the cost function above overall.
This is a classic assignment problem, which can be solved efficiently. I created a cost matrix filled with $c(t, s)$ values for all token–symbol pairs and solved it using SciPy's linear_sum_assignment.
Here’s an excerpt from the resulting assignment:
| Token | Symbol |
|---|---|
| have | bda |
| has | ada |
| had | bdad |
| become | bdBa |
| became | bdBc |
| went | bdbA |
| saw | bdBb |
| are | bdb |
| were | bdac |
| was | bD |
| is | bd |
| 's | bcb |
| taken | bdCa |
| took | bdaA |
| take | bdcc |
| taking | bdaD |
| bring | bdDa |
| brought | bdDb |
| came | bdDc |
| come | bddd |
| ... | ... |
And here are the shortest symbols (3 dots or fewer) and their assigned tokens:
| Token | Symbol |
|---|---|
| the | a |
| . | b |
| s | c |
| , | d |
| i | A |
| c | B |
| re | C |
| y | D |
| " | aa |
| t | ab |
| that | ac |
| it | ad |
| to | ba |
| d | bb |
| a | bc |
| is | bd |
| - | ca |
| ing | cb |
| and | cc |
| of | cd |
| ed | da |
| on | db |
| for | dc |
| in | dd |
Notice that similar words (e.g., “become” and “became”) have similar symbols (“bdBa” and “bdBc”) assigned, while more frequent words (e.g., “is” and “was”) have shorter symbols (“bd” and “bD”) assigned. You can find the full list of all token–symbol assignments here.
NeuralMorse in Action
You can generate and listen to NeuralMorse for any input text using this Google Colab notebook. All the data and inference code are available in this GitHub repository.
Discussion
The most important question, I think, is this: Can humans learn to decode NeuralMorse by ear after training? When you first hear an encoded sentence, it sounds like a random sequence of musical notes, and decoding it in real time seems daunting.
However, I’ve listened to a bunch of sentences for a while and it started to make some sense, partially because you start to remember some frequent patterns (“the” “you” “-s” etc.). This experience is very similar to learning a new language, but the learning curve feels dramatically faster. Designing effective training materials for NeuralMorse (something like Google’s Morse Typing Trainer) would be a fascinating and important next step.
It’s also worth noting that the current version of NeuralMorse is tailored specifically to English. But the same approach could be used to create similar encoding systems for other languages. Even more interesting is to design a multilingual version of this, where words with similar meanings sound similar regardless of their languages.
Finally, the framework I presented—statistical tokenization followed by assignment via optimization—isn’t specific to Morse code or even to sound. These techniques could be used to “re-invent” other forms of text encoding. For example, redesigning Braille using variable-length symbols could be both interesting and practical. I’ll leave that for future exploration.
Notes
* Note 1: This pitch scale happens to match the basic tuning of the pipa, a traditional Chinese musical instrument that my wife is learning. These elements can be mapped to any notes as long as they are distinguishable by the human ear—you could even assign them to different notes of a chord (e.g., Dm7, G7, Cmaj7) and change the chord dynamically to make the output sound more musical.
* Note 2: I used 1,900 unique tokens instead of 1,800 to account for the additional tokens that begin with “▁” (representing whitespace) generated by SentencePiece. As a post-processing step, I forced the tokenization of whitespace, reducing the vocabulary size by about 100.
* Note 3: I realized there was a serious bias issue when training on just 1/100th of OpenWebText2. Specifically:
Because OpenWebText2 includes text only up to early 2020, it underrepresents newer words like “Biden” and “2021.” To address this, I supplemented the dataset with high-ranking Reddit posts from 2021.
The SentencePiece model trained on OpenWebText2 was not gender-fair—I noticed that many female names and gendered terms (e.g., “sister,” “wife,” “daughter”) were missing from the dictionary, meaning they would require longer encodings. To mitigate this, I oversampled sentences containing words like “she” and “her” during training. This reduced the bias somewhat, though it didn’t eliminate it completely.